The Queens Puzzle in QBasic
Home › Forums › Previous Months › 33 – October 2019: The 7th Guest › The Queens Puzzle in QBasic
- This topic has 5 replies, 4 voices, and was last updated 6 years, 3 months ago by
 evilcommiedictator.
evilcommiedictator.
-

sorceressParticipantOctober 4, 2019 at 7:01 pm #2918B = 8
bFact = 1: FOR i = 1 TO B: bFact = bFact * i: NEXT
DIM Q(16) AS LONG
FOR i = 0 TO B: Q(i) = i: NEXT ‘initial permutationFOR n = 1 TO bFact – 1
‘permutations guarantee queens are on unique rows and columns
‘we only need to check diagonals
ok = 1
FOR i = 0 TO B – 2: FOR j = i + 1 TO B – 1
IF ABS(Q(j) – Q(i)) = j – i THEN ok = 0
NEXT: NEXT‘print the permutation if it is a solution
IF ok = 1 THEN
s = s + 1
COLOR 7, 0: LOCATE 1, 1: PRINT “Solution: “; s
FOR y = 0 TO B – 1: FOR x = 0 TO B – 1
COLOR 14, 6 + ((x + y) MOD 2)
IF Q(y) = x THEN PRINT ” Q “; ELSE PRINT ” “;
NEXT: PRINT: NEXT
SLEEP
END IF‘advance to the next permutation
i = B – 1: WHILE Q(i – 1) > Q(i): i = i – 1: WEND: mLo = i – 1
i = B – 1: WHILE Q(i) < Q(mLo): i = i – 1: WEND: mHi = i
k = Q(mLo): Q(mLo) = Q(mHi): Q(mHi) = k
i = mLo + 1: j = B – 1
WHILE i < j
k = Q(i): Q(i) = Q(j): Q(j) = k
i = i + 1: j = j – 1
WENDNEXT
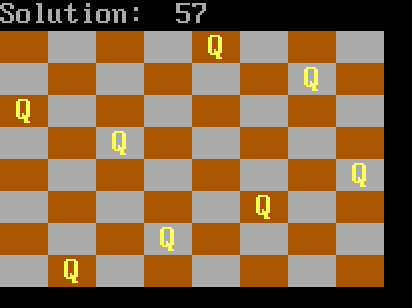 October 7, 2019 at 8:52 pm #2922
October 7, 2019 at 8:52 pm #2922I’ll just stick with running GORILLAS.BAS thanks 🙂

sorceressParticipantOctober 12, 2019 at 4:43 pm #2925In the mathematical spirit of the puzzle, we can determine the number of solutions for different board sizes. Consider placing N queens on an NxN board:
N _ # Solutions _ as a % of all possible permutations
1 _ 1 _ 100%
2 _ 0 _ 0%
3 _ 0_ 0%
4 _ 2 _ 8.33%
5 _ 10 _ 8.33%
6 _ 4 _ 0.56%
7 _ 40 _ 0.79%
8 _ 92 _ 0.23%
9 _ 352 _ 0.097%
10 _ 724 _ 0.020%
11 _ 2680 _ 0.0067%
12 _ 14200 _ 0.0030%
13 _ 73712 _ 0.0012%
14 _ 365596 _ 0.00042%
15 _ 2279184 _ 0.00017%The percentages in some way reflect the difficulty of finding a solution to each puzzle grid.

sorceressParticipantOctober 19, 2019 at 6:47 pm #2933The next obvious task is to find a solution to the general case, given any N>3.
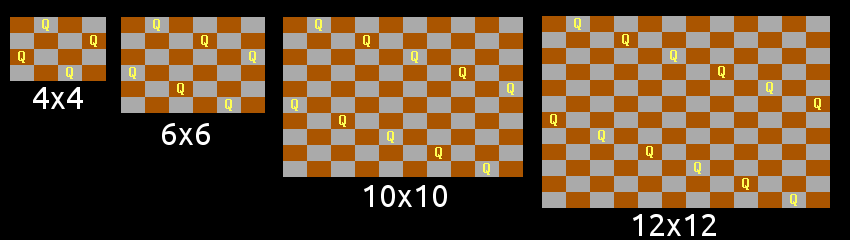
I have found that some solutions create a pattern on the board which could be extended into solutions over larger boards.
For example, for even values of N, there is this very simple pattern of queens placed in two lines of “knights moves”. There is an exception however – it only works for N congruent to 0 or 4 mod 6, and not for 2 mod 6:
The pattern doesn’t work for N congruent to 2 mod 6, because of a diagonal clash between the two lines, as is discovered in the original N=8 problem.
It is seen that queens placed in a line of “knights moves” occupy a diagonal every three diagonals, and that a second such line will stand in opposition to the first line in 1 out of 3 even-sized boards, which is where my “mod 6” comes from.
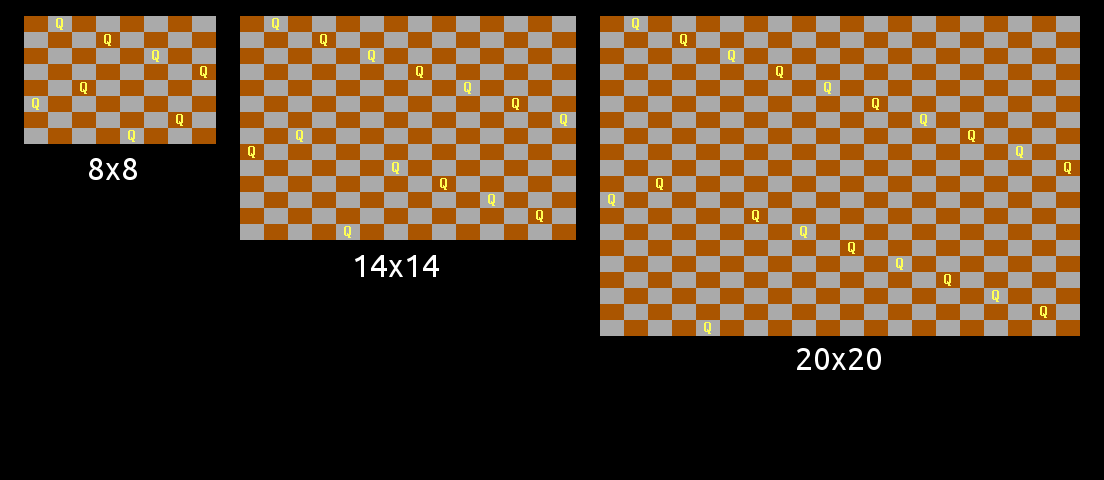
However, with a small tweak to the pattern, I found it could be salvaged:
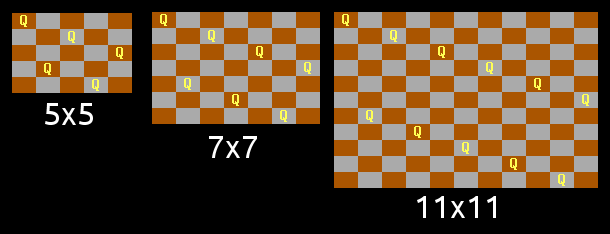
For odd N, a similar line pattern was found by swapping the two lines around, but this only works for N congruent to 1 or 5 mod 6. (The diagonals present the same problem in the 3 mod 6 case):
This leaves only the class N congruent to 3 mod 6, which caused me some head-scratching. But with a tweak similar to the 2 mod 6 case, albeit a little more complex, a working pattern was found:
So this provides a solution to all NxN boards, except for the two impossible cases (N=2 and N=3).

dr_stParticipantOctober 22, 2019 at 11:32 am #2939Awesome analysis! I love working generalization and complete problem solutions. 🙂
October 24, 2019 at 11:16 am #2952Nice work Sorceress! Sadly I was on the knight spacing but couldn’t get it to work, then just stumbled onto the solution 🙁
You must be logged in to reply to this topic.
Home › Forums › Previous Months › 33 – October 2019: The 7th Guest › The Queens Puzzle in QBasic